Função TAXA do Excel aprenda como usar
A função TAXA do Excel calcula a taxa de juros necessária para pagar uma quantia especificada de um empréstimo. E semelhantemente, faz cálculos para atingir um valor teórico em um investimento, durante um determinado período.
Se os resultados sucessivos da função TAXA não convergirem para 0,0000001 depois de 20 iterações, TAXA retornará o valor de erro #NÚM!.
Se TAXA for a única variável desconhecida, podemos usar a função TAXA para calcular a taxa de juros.
Sintaxe da função TAXA do Excel
Taxa (nper, pgto, VP, [vf], [tipo], [suposição])
Nota: Consulte a função VP para obter uma descrição completa dos argumentos nper, pgto, vp, vf e tipo. Estas funções trabalham em conjunto e nós vamos aprender cada uma delas.
A sintaxe da função TAXA tem os seguintes argumentos:
Argumentos Obrigatórios:
Nper: o número total de períodos de pagamento em uma anuidade.
Pgto: o pagamento feito em cada período e não pode mudar durante a vigência da anuidade. Geralmente, pgto inclui o principal e os juros e nenhuma outra taxa ou tributo. Se pgto for omitido, você deverá incluir o argumento vf.
Vp: valor presente - o valor total correspondente ao valor atual de uma série de pagamentos futuros.
Argumentos Opcionais:
Vf: valor futuro, ou o saldo, que você deseja obter depois do último pagamento. Se vf for omitido, será considerado 0 o valor futuro de um empréstimo, por exemplo, é zero. Se vf for omitido, deve-se incluir o argumento pgto.
Tipo: número 0 ou 1 e indica as datas de vencimento.
Definir tipo para 0 ou omitido, no final do período e 1, para o início do período
Estimativa: a sua estimativa para a taxa.
NOTA: se você omitir estimativa, este argumento será considerado 10%.
Se TAXA não convergir, atribua valores diferentes para estimativa. Em geral, TAXA converge se estimativa estiver entre 0 e 1.
Exemplo da função TAXA do Excel
Faça o exemplo em uma tabela de Excel. Copie os dados de exemplo da tabela a seguir e cole-os na célula A1 de uma nova planilha do Excel. Depois copie e cole as funções a seguir, nas células indicadas também a seguir logo depois da tabela.
| Função TAXA | ||
|---|---|---|
| Dados | Descrição | |
| 2 | Os anos do empréstimo | |
| R$ 500,00 | O pagamento mensal | |
| R$ 10.000,00 | A quantia do empréstimo | |
| Fórmula | Descrição | Resultado |
| TAXA(A3*12; -A4; A5) | Taxa mensal do empréstimo com os termos inseridos como argumentos em A3:A5. | 2% |
| TAXA(A3*12;- A4; A5)*12 | Taxa anual do empréstimo com os mesmos termos. | 18% |
=TAXA(A3*12; -A4; A5) cole na célula: C7
=TAXA(A3*12;- A4; A5)*12 cole na célula: C8
Você pode BAIXAR AQUI, um exemplo prático, em Excel, que compara e calcula um empréstimo, a planilha tem o formato da imagem abaixo.
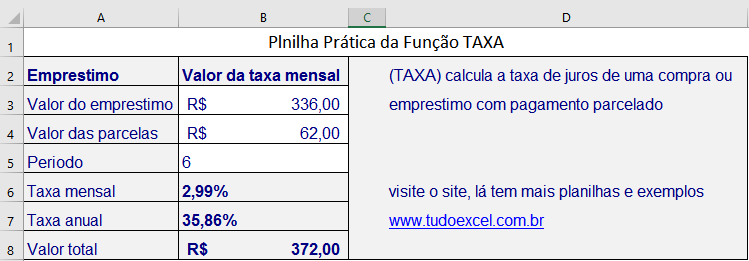
Uma dica Importante: Se você não quiser usar o sinal - menos, dentro da função, você pode usá-lo, no pagamento mensal, com o valor negativo.
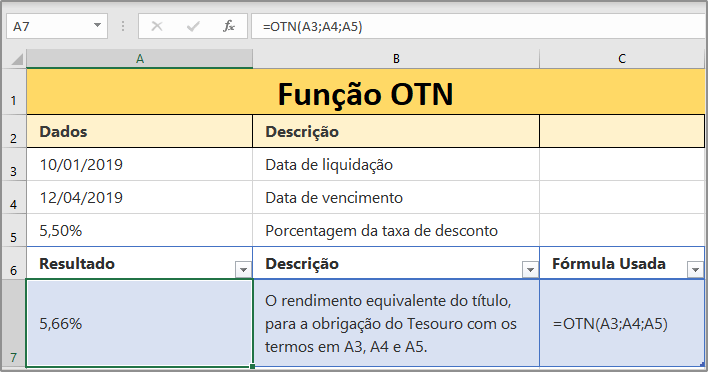
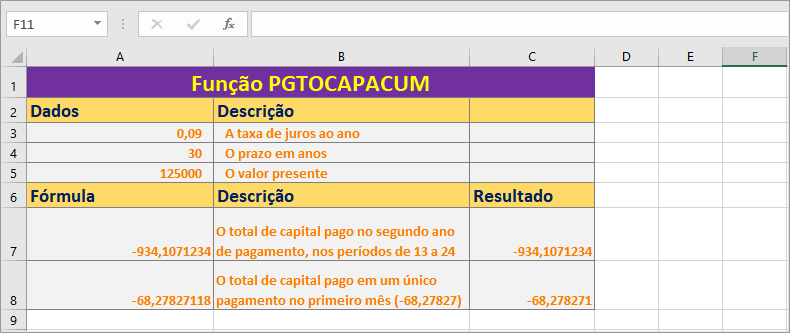
Recomendamos, que você leia outras funções de taxas no Excel, para interagir com cálculos em funções financeiras. Existem outras fórmulas em que a taxa de juros é calculada, como porcentagens, valor futuro e valor presente.




Olà, tudo bem, TB dou amante de tecnologia, abaixo minha dúvida.
Se vf for omitido, deve-se incluir o argumento pgto.
Entendo que uso VF ou PGTO.
Agora já observou que se usar a PGTO e fizer o mesmo cálculo com VF, não encontramos o mesmo percentual. Daí fica a dúvida por que isso acontece?
Sei que o cálculo está certo usando o VF, por que usei a fórmula de Juros composto pra confirmar.
São funções diferentes!
Boa tarde.
O Bruno está correto a formula não calcula alguns valores e ocorre o erro #NUM.
O exemplo que ele deu é totalmente aplicável na planilha que você deixou para download.
Valor 1450,00 em 12x de 415,28
Mas também serve para outros exemplos:
Valor 1000,00 em 200x de 100. O juros mensal sempre fica em 10%, mesmo se colocar em 300x Valor 500,00 em 10x de 300, o resultado é #NÚM!
Gostaria de entender porque isso acontece.
Oi Leandro Rocha, eu estou fiquei mais de 4 horas (sábado) tentando descobrir o erro e não consegui. Até peço desculpas ao Bruno, porque eu disse que o Excel calcula corretamente e que o erro poderia estar com o Bruno. Mas eu verifiquei no próprio exemplo da Microsoft e o erro persiste. Busquei em vários sites, inclusive internacionais e o erro também persiste.
Em todos os sites que eu pesquisei, encontre esta mesma explicação:
"#NUM! erro - Se os resultados de RATE não convergirem após 20 iterações, TAXA retornará #NUM! valor de erro." Mas não diz o porquê!
Isso pode ser causado pela falha em usar o sinal negativo ou positivo em relação às convenções de fluxo de caixa. Só que eu ainda não entendi porque acontece, já que na fórmula o sinal de menos antes do pagamento mensal pode mudar o critério (positivo, negativo)
Se alguém souber aí por favor adicione no comentário... Mesmo assim vou continuar investigando. Tem que haver uma solução. Como estou te respondendo no Domingo pela manhã, tentarei outro dia.
Boa tarde Edivaldo, como calculo em uma calculadora o que a função TAXA faz? Por favor
Oi Ivan. Eu sei na função TAXA na planilha
Há um erro na taxa anual, o ideal seria a fórmula =((1+TAXA(A3*12;- A4; A5))^12)-1. O cálculo anual estava contemplando juros simples, essa é a fórmula para juros compostos.
Oi Yuri De Martino. Obrigado pelo seu feedback. A fórmula adicionada é totalmente criada pelo Excel e está nos tutoriais do MS Office. Mesmo assim vou analisar, fazer testes e, se caso funcionar, publicarei no artigo.
Boa tarde... com alguns valores ele não calcula.
Por exemplo, empréstimo da Crefisa, Valor 1450,00 em 12x de 415,28, ele não consegue calcular, retorna #NUM.
Sabe como resolver isso?
Obrigado
Oi Bruno. Tem que verificar qual é o erro aí. A função TAXA calcula corretamente, sempre.