Confira Dicas de Funções Financeiras do Excel

Confira dicas de funções financeiras do Excel com tutorial completo sobre VP, VF, PGTO, TIR, VPL e outras ferramentas essenciais. Aprenda a calcular investimentos, financiamentos, empréstimos e análises de viabilidade econômica com exemplos práticos para tomada de decisões financeiras inteligentes.

As funções financeiras do Excel são ferramentas indispensáveis para profissionais que lidam com análise de investimentos, planejamento financeiro, avaliação de projetos e gestão de recursos. Essas funcionalidades transformam o Excel em uma verdadeira calculadora financeira avançada, capaz de resolver desde cálculos simples de juros até análises complexas de viabilidade econômica de grandes empreendimentos.

Por exemplo: nós fazemos pagamentos mensais, por isso usamos 6%/12 = 0,5% para taxa e 20 * 12 = 240 para Nper, que é o número total de pagamentos pelo empréstimo. Se efetuar pagamentos anuais do mesmo empréstimo, usamos 6% para taxa e 20 para Nper, que será 20 anos. Entendeu? Então vamos continuar e aprender dicas de funções financeiras do Excel com exemplos práticos.

O Que São Funções Financeiras do Excel e Por Que Utilizá-las

As funções financeiras do Excel são fórmulas predefinidas especializadas em cálculos relacionados ao valor do dinheiro no tempo, permitindo que você resolva problemas complexos de matemática financeira com apenas alguns cliques. Diferentemente das funções básicas de soma ou média, essas ferramentas consideram variáveis cruciais como taxas de juros, períodos de tempo e fluxos de caixa para fornecer resultados precisos.

O conceito fundamental por trás dessas funções é que o dinheiro possui valor temporal - ou seja, R$ 1.000 hoje valem mais do que R$ 1.000 daqui a um ano, devido à capacidade de investimento e geração de rendimentos. As funções financeiras do Excel automatizam os cálculos matemáticos necessários para quantificar essas diferenças temporais e ajudá-lo a tomar decisões informadas sobre investimentos, financiamentos e alocação de recursos.

Benefícios de dominar funções financeiras:

• Agilidade decisória: Avalia rapidamente múltiplos cenários de investimento sem cálculos manuais complexos.
• Precisão matemática: Elimina erros humanos em fórmulas extensas de juros compostos e amortização.
• Planejamento estratégico: Fundamenta decisões de longo prazo com dados concretos e simulações realistas.
• Análise comparativa: Facilita comparação entre diferentes propostas de financiamento ou oportunidades de aplicação.
• Profissionalização: Demonstra competência técnica em relatórios e apresentações para stakeholders.
• Economia de tempo: Automatiza cálculos que levariam horas para serem concluídos manualmente.

Principais categorias de funções financeiras:

Categoria	Funções Principais	Aplicação Típica
Valor no Tempo	VP, VF, NPER	Cálculo de poupança e investimentos futuros
Pagamentos	PGTO, PPGTO, IPGTO	Análise de prestações e financiamentos
Análise de Investimentos	VPL, TIR, MTIR	Avaliação de projetos e viabilidade econômica
Depreciação	BD, BDD, SLN	Cálculo de perda de valor de ativos
Títulos e Juros	TAXA, TAXAJUROS	Análise de rendimentos de aplicações

Veja Algumas Dicas de Funções Financeiras do Excel Mias Usadas

1. Função VP: Como Calcular o Valor Presente de Investimentos

A função VP (Valor Presente) calcula quanto vale hoje um conjunto de pagamentos futuros, considerando uma taxa de juros específica. Essa função é fundamental para avaliar se um investimento ou aplicação financeira faz sentido econômico, comparando o valor investido hoje com o retorno esperado no futuro trazido a valor presente.

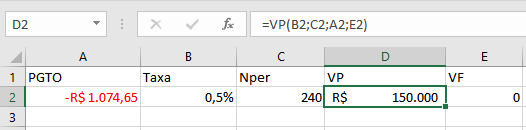
Quando você recebe uma proposta de investimento que promete retornar determinado valor ao longo dos anos, a função VP responde à pergunta crucial: "Quanto esse fluxo de pagamentos futuros vale em dinheiro de hoje?" Isso permite comparar oportunidades diferentes em uma base comum e decidir onde alocar seus recursos com maior inteligência financeira.

Sintaxe da função VP:

=VP(taxa; nper; pgto; [vf]; [tipo])

Parâmetros detalhados:

• taxa: Taxa de juros por período (se anual e períodos mensais, divida por 12).
• nper: Número total de períodos de pagamento.
• pgto: Valor do pagamento em cada período (deve ser negativo se for saída de caixa).
• vf: [Opcional] Valor futuro ou saldo final após o último pagamento (padrão é 0).
• tipo: [Opcional] 0 para pagamentos no final do período, 1 para início (padrão é 0).

Exemplo prático 1: Quanto investir hoje para receber R$ 500 mensais por 5 anos?

Dados:
- Pagamentos mensais: R$ 500
- Prazo: 5 anos (60 meses)
- Taxa de juros: 0,8% ao mês
- Tipo: Pagamentos no final do mês

Fórmula:
=VP(0,8%; 60; -500; 0; 0)

Resultado: R$ 24.204,18

Interpretação: Você precisaria investir R$ 24.204,18 hoje para receber R$ 500 mensais durante 5 anos, considerando rendimento de 0,8% ao mês.

Exemplo prático 2: Avaliar proposta de plano de previdência:

Parâmetro	Valor
Contribuição mensal	R$ 800
Prazo de contribuição	20 anos (240 meses)
Taxa de retorno estimada	0,6% ao mês
Valor futuro garantido	R$ 50.000

Fórmula:
=VP(0,6%; 240; -800; 50000; 0)
Resultado: R$ 118.347,92

Dicas importantes para usar VP:

• Sinais corretos: Use valores negativos para dinheiro que sai e positivos para dinheiro que entra.
• Consistência temporal: Mantenha taxa e períodos na mesma unidade (ambos mensais ou ambos anuais).
• Taxa real versus nominal: Considere inflação ao definir taxa de desconto para análises realistas.
• Comparação de alternativas: Use VP para avaliar qual investimento oferece melhor valor presente líquido.

Aplicações práticas no dia a dia:

• Avaliar se vale a pena comprar à vista com desconto ou financiar em parcelas.
• Calcular quanto precisa investir hoje para ter determinada renda na aposentadoria.
• Comparar propostas de planos de previdência privada de diferentes instituições.
• Determinar o valor justo de um título de renda fixa com pagamentos periódicos.

2. Função VF: Como Calcular o Valor Futuro de Aplicações

A função VF (Valor Futuro) calcula quanto uma aplicação financeira valerá no futuro, considerando depósitos regulares e uma taxa de juros consistente ao longo do tempo. Essa ferramenta é essencial para planejamento de longo prazo, permitindo visualizar o crescimento do patrimônio e estabelecer metas financeiras realistas baseadas em contribuições mensais.

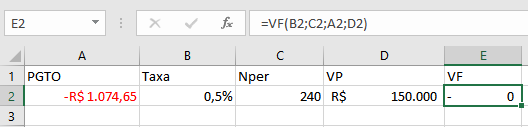
Diferentemente da função VP que traz valores futuros para o presente, a VF projeta valores atuais para o futuro, respondendo perguntas como "Se eu poupar R$ 500 por mês durante 10 anos com rendimento de 0,7% ao mês, quanto terei acumulado?" Essa perspectiva é fundamental para quem deseja construir reservas financeiras, planejar aposentadoria ou criar fundos específicos para objetivos de médio e longo prazo.

Sintaxe da função VF:

=VF(taxa; nper; pgto; [vp]; [tipo])

Detalhamento dos argumentos:

• taxa: Taxa de juros por período (expressa em decimal ou percentual).
• nper: Número total de períodos de capitalização.
• pgto: Valor do pagamento regular em cada período (negativo para aplicações).
• vp: [Opcional] Valor presente ou montante inicial investido (padrão é 0).
• tipo: [Opcional] 0 para depósitos no fim do período, 1 para início (padrão é 0).

Exemplo prático 1: Quanto terei economizado em 3 anos poupando R$ 1.000 mensalmente?

Dados:
- Depósito mensal: R$ 1.000
- Prazo: 3 anos (36 meses)
- Taxa de rendimento: 0,5% ao mês
- Investimento inicial: R$ 0
- Depósitos no final do mês

Fórmula:
=VF(0,5%; 36; -1000; 0; 0)

Resultado: R$ 39.336,10

Análise: Depositando R$ 1.000 mensalmente por 36 meses a 0,5% ao mês, você acumulará R$ 39.336,10 (total depositado: R$ 36.000 + R$ 3.336,10 de juros).

Exemplo prático 2: Crescimento de investimento inicial com aportes mensais:

Elemento	Valor
Capital inicial	R$ 10.000
Aporte mensal	R$ 500
Prazo	5 anos (60 meses)
Rentabilidade mensal	0,8%

Fórmula:
=VF(0,8%; 60; -500; -10000; 0)
Resultado: R$ 56.385,79

Detalhamento: Investindo R$ 10.000 inicialmente mais R$ 500 mensais por 5 anos a 0,8% ao mês, você terá R$ 56.385,79 (R$ 40.000 de aportes + R$ 16.385,79 de rendimentos).

Tabela comparativa de cenários:

Aporte Mensal	Prazo	Taxa Mensal	Valor Futuro
R$ 300	10 anos	0,6%	R$ 49.865,52
R$ 500	10 anos	0,6%	R$ 83.109,20
R$ 1.000	10 anos	0,6%	R$ 166.218,40
R$ 1.000	15 anos	0,6%	R$ 290.663,17

Estratégias práticas com VF:

• Simulação de metas: Defina objetivo financeiro e ajuste aportes necessários para alcançá-lo.
• Comparação de produtos: Avalie diferentes aplicações financeiras projetando valor final acumulado.
• Planejamento de aposentadoria: Estime quanto terá disponível ao parar de trabalhar mantendo contribuições regulares.
• Criação de fundos específicos: Calcule quanto poupar mensalmente para comprar um imóvel, carro ou fazer viagem.

3. Função PGTO: Como Calcular Parcelas de Financiamentos

A função PGTO calcula o valor da prestação fixa de um financiamento ou empréstimo, considerando taxa de juros constante e número definido de parcelas. Essa é provavelmente a função financeira mais utilizada no dia a dia, essencial para quem está comprando imóveis, veículos ou qualquer bem através de financiamento com sistema de amortização constante.

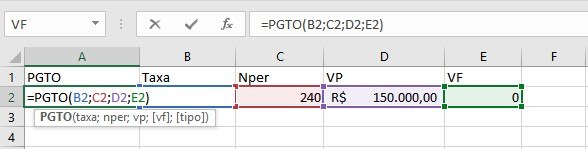
Quando você precisa saber exatamente quanto pagará mensalmente em um financiamento, a função PGTO fornece a resposta instantaneamente, permitindo avaliar se a prestação cabe no orçamento familiar ou empresarial. Além disso, essa função ajuda a comparar propostas de diferentes instituições financeiras e negociar melhores condições baseando-se em cálculos precisos e transparentes.

Sintaxe da função PGTO:

=PGTO(taxa; nper; vp; [vf]; [tipo])

Explicação dos parâmetros:

• taxa: Taxa de juros por período (mensal, anual, etc.).
• nper: Número total de pagamentos.
• vp: Valor presente ou principal do empréstimo (valor financiado).
• vf: [Opcional] Saldo residual após último pagamento (geralmente 0).
• tipo: [Opcional] 0 para pagamentos no final, 1 para início do período.

Exemplo prático 1: Calcular prestação de financiamento imobiliário:

Dados:
- Valor financiado: R$ 350.000
- Taxa de juros: 0,75% ao mês
- Prazo: 30 anos (360 meses)
- Saldo final: R$ 0
- Pagamento no fim do mês

Fórmula:
=PGTO(0,75%; 360; 350000; 0; 0)

Resultado: -R$ 2.709,06

Interpretação: A prestação mensal será de R$ 2.709,06 (valor negativo indica saída de dinheiro).

Exemplo prático 2: Financiamento de veículo com entrada:

Item	Valor
Preço do veículo	R$ 85.000
Entrada (30%)	R$ 25.500
Valor financiado	R$ 59.500
Taxa de juros	1,2% ao mês
Prazo	48 meses

Fórmula:
=PGTO(1,2%; 48; 59500; 0; 0)

Resultado: -R$ 1.657,39

Comparação de cenários de financiamento:

Prazo	Taxa	Parcela Mensal	Total Pago	Total de Juros
24 meses	1,2%	R$ 2.821,65	R$ 67.719,60	R$ 8.219,60
36 meses	1,2%	R$ 2.011,47	R$ 72.412,92	R$ 12.912,92
48 meses	1,2%	R$ 1.657,39	R$ 79.554,72	R$ 20.054,72
60 meses	1,2%	R$ 1.451,78	R$ 87.106,80	R$ 27.606,80

Aplicações avançadas da função PGTO:

• Análise de capacidade de pagamento: Determine valor máximo de financiamento baseado em parcela que cabe no orçamento.
• Negociação de condições: Simule diferentes combinações de prazo e taxa para encontrar melhor proposta.
• Planejamento de amortização: Use com PPGTO e IPGTO para criar tabelas detalhadas de quitação.
• Avaliação de leasing: Compare custo de aluguel operacional versus compra financiada.

Dicas para otimizar uso da função:

• Impacto do prazo: Prazos maiores reduzem parcela mas aumentam juros totais significativamente.
• Entrada maior: Reduzir valor financiado (aumentar entrada) diminui prestação e custo total de juros.
• Antecipação: Calcule nova prestação ao antecipar parcelas usando PGTO com nper reduzido.
• Simulação de renegociação: Avalie benefício de refinanciar dívida com taxa menor em nova instituição.

4. Função IPGTO: Como Calcular a Parte de Juros das Parcelas

A função IPGTO calcula especificamente o valor dos juros embutido em uma determinada parcela de um financiamento ou empréstimo, permitindo separar o que você está pagando de juros daquilo que está efetivamente amortizando do principal. Essa função é fundamental para entender a composição real de cada prestação e para fins de declaração de imposto de renda quando juros são dedutíveis.

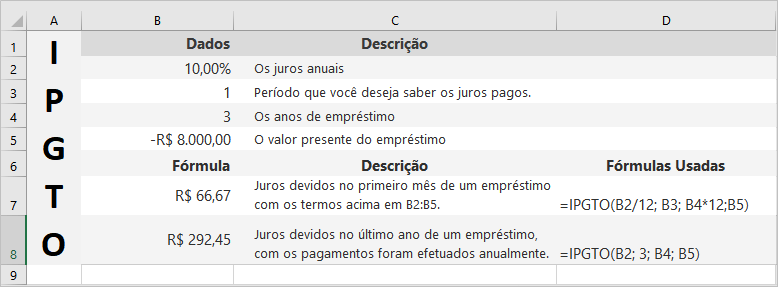
Nos primeiros meses de um financiamento de longo prazo, a maior parte da prestação corresponde a juros, e apenas uma pequena fração reduz o saldo devedor principal. Com o passar do tempo, essa proporção se inverte gradualmente. A função IPGTO permite visualizar essa dinâmica em qualquer momento do financiamento, revelando exatamente quanto está sendo pago de juros em cada período específico.

Sintaxe da função IPGTO:

=IPGTO(taxa; per; nper; vp; [vf]; [tipo])

Descrição dos argumentos:

• taxa: Taxa de juros por período.
• per: Período específico para o qual você quer calcular os juros (1 para primeira parcela, 2 para segunda, etc.).
• nper: Número total de períodos de pagamento.
• vp: Valor presente ou principal do empréstimo.
• vf: [Opcional] Saldo residual desejado (geralmente 0).
• tipo: [Opcional] 0 para pagamentos no final do período, 1 para início.

Exemplo prático 1: Juros da primeira versus última parcela de financiamento:

Dados do financiamento:
- Valor: R$ 200.000
- Taxa: 0,8% ao mês
- Prazo: 240 meses (20 anos)
- Sistema: Price (parcelas fixas)

Juros na 1ª parcela:
=IPGTO(0,8%; 1; 240; 200000; 0; 0)
Resultado: -R$ 1.600,00

Juros na 240ª parcela:
=IPGTO(0,8%; 240; 240; 200000; 0; 0)
Resultado: -R$ 13,48

Análise: Na primeira parcela, R$ 1.600 são juros (80% da prestação), enquanto na última apenas R$ 13,48, mostrando como amortização aumenta ao longo do tempo.

Exemplo prático 2: Criar tabela de juros anuais para IR:

Ano	Parcelas	Fórmula Total de Juros	Juros Anuais
1	1 a 12	=SOMASES(IPGTO(...))	R$ 18.450,32
2	13 a 24	=SOMASES(IPGTO(...))	R$ 16.892,17
3	25 a 36	=SOMASES(IPGTO(...))	R$ 15.201,85

Tabela completa de evolução de uma parcela:

Parcela	Valor Total	Juros (IPGTO)	Amortização (PPGTO)	Saldo Devedor
1	R$ 2.092,00	R$ 1.600,00	R$ 492,00	R$ 199.508,00
12	R$ 2.092,00	R$ 1.525,11	R$ 566,89	R$ 192.891,45
60	R$ 2.092,00	R$ 1.113,38	R$ 978,62	R$ 137.110,22
120	R$ 2.092,00	R$ 662,70	R$ 1.429,30	R$ 80.547,63
240	R$ 2.092,00	R$ 13,48	R$ 2.078,52	R$ 0,00

Usos práticos da função IPGTO:

• Declaração de IR: Calcular juros dedutíveis de financiamento imobiliário com recursos do FGTS.
• Análise de custo efetivo: Visualizar quanto se paga de juros versus amortização ao longo do tempo.
• Simulação de antecipação: Avaliar economia de juros ao quitar parcelas específicas antecipadamente.
• Contabilidade empresarial: Segregar despesa financeira da redução de passivo nos registros contábeis.

Combinação com outras funções financeiras:

Prestação total = PGTO(taxa; nper; vp)
Juros da parcela = IPGTO(taxa; per; nper; vp)
Amortização = PPGTO(taxa; per; nper; vp)

Verificação: PGTO = IPGTO + PPGTO

5. Função PPGTO: Como Calcular a Amortização do Principal

A função PPGTO calcula especificamente a parte da prestação que efetivamente reduz o saldo devedor do empréstimo ou financiamento, ou seja, quanto você está realmente abatendo do valor original que pegou emprestado. Essa função complementa perfeitamente a IPGTO, permitindo uma visão completa da composição de cada parcela entre juros e amortização.

Entender quanto de cada pagamento está realmente reduzindo sua dívida é essencial para planejamento financeiro de longo prazo, especialmente em financiamentos extensos como imobiliários onde essa proporção muda dramaticamente ao longo dos anos. A função PPGTO revela que nos primeiros anos você está "pagando para usar o dinheiro" (juros) mais do que efetivamente "pagando a dívida" (amortização).

Sintaxe da função PPGTO:

=PPGTO(taxa; per; nper; vp; [vf]; [tipo])

Parâmetros explicados:

• taxa: Taxa de juros por período aplicada ao financiamento.
• per: Número da parcela específica que você quer analisar.
• nper: Total de parcelas do financiamento.
• vp: Valor presente ou montante total financiado.
• vf: [Opcional] Saldo residual final desejado (padrão 0).
• tipo: [Opcional] 0 para pagamentos ao final do período, 1 para início.

Exemplo prático 1: Evolução da amortização em financiamento de veículo:

Dados:
- Valor financiado: R$ 60.000
- Taxa: 1,5% ao mês
- Prazo: 48 meses
- Prestação fixa: R$ 1.787,62 (calculada com PGTO)

Amortização na 1ª parcela:
=PPGTO(1,5%; 1; 48; 60000)
Resultado: -R$ 887,62

Amortização na 24ª parcela:
=PPGTO(1,5%; 24; 48; 60000)
Resultado: -R$ 1.190,40

Amortização na 48ª parcela:
=PPGTO(1,5%; 48; 48; 60000)
Resultado: -R$ 1.761,33

Análise: A amortização começa em R$ 887,62 (menos da metade da prestação) e evolui até R$ 1.761,33 (quase a prestação inteira) na última parcela.

Tabela comparativa detalhada de composição das parcelas:

Parcela	Prestação Total	Juros	Amortização	% Amortização	Saldo Devedor
1	R$ 1.787,62	R$ 900,00	R$ 887,62	49,7%	R$ 59.112,38
6	R$ 1.787,62	R$ 827,12	R$ 960,50	53,7%	R$ 54.280,75
12	R$ 1.787,62	R$ 736,26	R$ 1.051,36	58,8%	R$ 48.333,09
24	R$ 1.787,62	R$ 597,22	R$ 1.190,40	66,6%	R$ 38.592,18
36	R$ 1.787,62	R$ 434,18	R$ 1.353,44	75,7%	R$ 27.557,71
48	R$ 1.787,62	R$ 26,29	R$ 1.761,33	98,5%	R$ 0,00

Exemplo prático 2: Calcular quanto será amortizado em um ano específico:

Para somar amortização do ano 2 (parcelas 13 a 24):

Opção 1 - Soma individual:
=PPGTO(1,5%; 13; 48; 60000) + PPGTO(1,5%; 14; 48; 60000) + ... + PPGTO(1,5%; 24; 48; 60000)

Opção 2 - Usar fórmula matricial:
=SOMARPRODUTO(PPGTO(1,5%; LIN(13:24); 48; 60000))

Resultado: -R$ 13.876,23 amortizados no segundo ano

Aplicações estratégicas da função PPGTO:

• Planejamento de quitação: Calcule saldo devedor após determinado número de pagamentos para negociar quitação.
• Análise de portabilidade: Compare quanto já foi amortizado versus quanto ainda falta para decidir sobre refinanciamento.
• Gestão de fluxo de caixa: Entenda quando a maior parte do pagamento começa a reduzir dívida efetivamente.
• Decisão de antecipação: Avalie se vale mais antecipar parcelas iniciais (muitos juros) ou finais (muita amortização).

Relacionamento entre PGTO, IPGTO e PPGTO:

Verificação matemática sempre verdadeira:
PGTO(taxa; nper; vp) = IPGTO(taxa; per; nper; vp) + PPGTO(taxa; per; nper; vp)

Exemplo na parcela 10:
R$ 1.787,62 = R$ 761,71 (juros) + R$ 1.025,91 (amortização)

6. Função NPER: Como Calcular Prazo de Investimentos e Financiamentos

A função NPER determina o número de períodos necessários para alcançar um objetivo financeiro específico, seja acumular determinado montante através de depósitos regulares ou quitar completamente um empréstimo com pagamentos fixos. Essa função inverte a lógica das anteriores, respondendo "quanto tempo vai levar" em vez de "quanto vai custar".

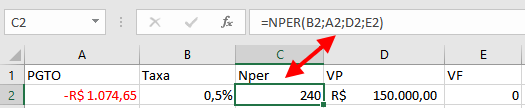
Quando você tem meta financeira clara mas não sabe quanto tempo levará para atingi-la mantendo determinado ritmo de poupança, a função NPER fornece a resposta precisa. Similarmente, se você quer saber em quantos meses conseguirá quitar uma dívida pagando parcelas de valor específico, essa função calcula exatamente o prazo necessário considerando os juros acumulados no período.

Sintaxe da função NPER:

=NPER(taxa; pgto; vp; [vf]; [tipo])

Detalhamento dos argumentos:

• taxa: Taxa de juros por período.
• pgto: Valor do pagamento em cada período (negativo para investimentos, positivo para recebimentos).
• vp: Valor presente ou montante inicial (principal de empréstimo ou investimento inicial).
• vf: [Opcional] Valor futuro desejado ou saldo residual final.
• tipo: [Opcional] 0 para pagamentos no final, 1 para início do período.

Exemplo prático 1: Quanto tempo para acumular R$ 100.000 poupando R$ 1.500 mensais?

Dados:
- Depósito mensal: R$ 1.500
- Taxa de rendimento: 0,6% ao mês
- Investimento inicial: R$ 0
- Meta: R$ 100.000

Fórmula:
=NPER(0,6%; -1500; 0; 100000; 0)

Resultado: 57,89 meses (aproximadamente 4 anos e 10 meses)

Análise: Investindo R$ 1.500 mensalmente com rendimento de 0,6% ao mês, você levará cerca de 58 meses para acumular R$ 100.000.

Exemplo prático 2: Prazo para quitar dívida com parcelas específicas:

Situação	Dados	Fórmula	Resultado
Dívida de cartão	Saldo: R$ 8.000, Parcela: R$ 500, Taxa: 10% mês	=NPER(10%; -500; 8000)	26,7 meses
Financiamento	Saldo: R$ 45.000, Parcela: R$ 1.200, Taxa: 1,2% mês	=NPER(1,2%; -1200; 45000)	45,3 meses
Empréstimo pessoal	Saldo: R$ 15.000, Parcela: R$ 800, Taxa: 2,5% mês	=NPER(2,5%; -800; 15000)	23,8 meses

Exemplo prático 3: Com investimento inicial, quanto tempo para aposentadoria?

Cenário:
- Capital inicial: R$ 50.000
- Aporte mensal: R$ 2.000
- Rentabilidade: 0,8% ao mês
- Objetivo: R$ 1.000.000

Fórmula:
=NPER(0,8%; -2000; -50000; 1000000; 0)

Resultado: 187,3 meses (aproximadamente 15 anos e 7 meses)

Aplicações práticas da função NPER:

• Planejamento de aposentadoria: Calcule quando terá capital suficiente mantendo aportes atuais.
• Metas de poupança: Determine prazo realista para objetivos como comprar imóvel, carro ou fazer viagem.
• Análise de dívidas: Descubra quanto tempo levará para se livrar completamente de financiamentos.
• Estratégia de antecipação: Compare prazos de quitação com e sem antecipação de parcelas.

Variações de cenários com NPER:

Situação base:
- Investir R$ 1.000/mês a 0,7% para atingir R$ 50.000

Sem investimento inicial:
=NPER(0,7%; -1000; 0; 50000) = 44,2 meses

Com R$ 10.000 inicial:
=NPER(0,7%; -1000; -10000; 50000) = 35,7 meses

Com R$ 20.000 inicial:
=NPER(0,7%; -1000; -20000; 50000) = 27,9 meses

Interpretação de resultados com casas decimais:

Quando NPER retorna 57,89 meses, isso significa:

• 57 meses completos de pagamento/investimento.
• Mais 0,89 de um mês adicional (aproximadamente 27 dias).
• Você pode arredondar para 58 meses para cálculos práticos.

7. Função TAXA: Como Calcular Taxa de Juros de Operações

A função TAXA calcula a taxa de juros por período de um financiamento ou investimento quando você conhece o valor das parcelas, o prazo e o montante envolvido. Essa função é extremamente útil para descobrir qual é a taxa real que uma instituição financeira está cobrando ou oferecendo, muitas vezes revelando custos ocultos em propostas aparentemente atrativas.

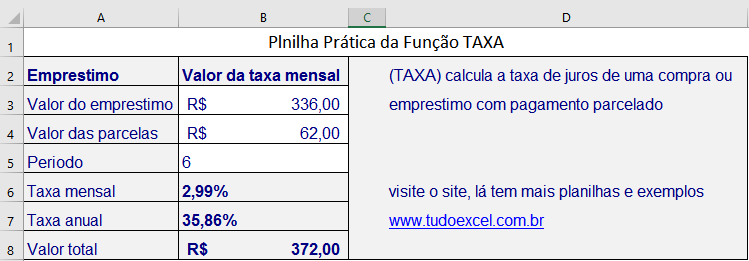
Diferente de simplesmente aceitar a taxa informada pela instituição, a função TAXA permite verificar matematicamente qual é o custo efetivo considerando todas as variáveis da operação. Isso é fundamental para comparar diferentes propostas de financiamento ou investimento em bases verdadeiramente equivalentes, evitando surpresas desagradáveis com juros embutidos que não foram claramente informados.

Sintaxe da função TAXA:

=TAXA(nper; pgto; vp; [vf]; [tipo]; [estimativa])

Explicação dos parâmetros:

• nper: Número total de períodos de pagamento.
• pgto: Valor do pagamento periódico.
• vp: Valor presente ou principal da operação.
• vf: [Opcional] Valor futuro ou saldo residual (padrão 0).
• tipo: [Opcional] 0 para pagamentos no final, 1 para início do período.
• estimativa: [Opcional] Taxa estimada inicial para cálculo iterativo (padrão 10%).

Exemplo prático 1: Descobrir taxa real de financiamento de veículo:

Proposta da loja:
- Preço do carro: R$ 70.000
- Entrada: R$ 20.000
- Valor financiado: R$ 50.000
- Parcelas: 48x de R$ 1.450

Fórmula:
=TAXA(48; -1450; 50000; 0; 0)

Resultado: 1,39% ao mês

Taxa anual equivalente:
=(1+1,39%)^12-1 = 18,05% ao ano

Análise: Embora a loja informe "juros baixos", a taxa efetiva de 1,39% ao mês (18,05% ao ano) pode ser superior a outras opções de financiamento bancário.

Exemplo prático 2: Verificar rentabilidade real de investimento:

Produto	Invest. Inicial	Valor Resgate	Prazo	Taxa Real (TAXA)
CDB Banco A	R$ 10.000	R$ 12.500	24 meses	0,95% ao mês
LCI Banco B	R$ 10.000	R$ 11.800	24 meses	0,70% ao mês
Tesouro Direto	R$ 10.000	R$ 13.200	24 meses	1,18% ao mês

Fórmula para CDB Banco A:
=TAXA(24; 0; -10000; 12500)
Resultado: 0,95% ao mês

Exemplo prático 3: Taxa efetiva de carnê com tarifa de cadastro:

Situação:
- Valor da compra: R$ 3.000
- Tarifa de cadastro: R$ 150
- Valor efetivamente recebido: R$ 2.850
- Parcelas: 12x de R$ 280

Cálculo considerando tarifa:
=TAXA(12; -280; 2850)
Resultado: 2,45% ao mês

Cálculo sem considerar tarifa (propaganda):
=TAXA(12; -280; 3000)
Resultado: 1,85% ao mês

Análise: A tarifa de cadastro aumenta a taxa efetiva de 1,85% para 2,45% ao mês, um custo adicional significativo raramente destacado.

Comparação de taxas em diferentes prazos:

Prazo	Parcela	Capital	Taxa Mensal	Taxa Anual
12 meses	R$ 900	R$ 10.000	1,20%	15,39%
24 meses	R$ 500	R$ 10.000	1,28%	16,48%
36 meses	R$ 365	R$ 10.000	1,35%	17,43%
48 meses	R$ 295	R$ 10.000	1,40%	18,16%

Dicas para uso eficiente da função TAXA:

• Convergência: Se retornar erro #NÚM!, forneça estimativa inicial diferente (3º parâmetro opcional).
• Taxas compostas: Para obter taxa anual de mensal, use =(1+taxa_mensal)^12-1.
• Incluir todos custos: Sempre considere tarifas, seguros e taxas extras no valor presente.
• Comparação justa: Converta todas taxas para mesma unidade temporal antes de comparar propostas.

Situações práticas de aplicação:

• Validar se taxa informada pela loja corresponde ao valor real das parcelas apresentadas.
• Calcular custo efetivo de crédito rotativo de cartão para comparar com empréstimo pessoal.
• Avaliar rentabilidade real de título de renda fixa antes de aplicar recursos.
• Descobrir taxa implícita em promoções tipo "compre hoje, pague em X meses sem juros".

8. Função VPL: Como Avaliar Viabilidade de Projetos e Investimentos

A função VPL (Valor Presente Líquido) é uma das ferramentas mais importantes para análise de viabilidade econômica de projetos, calculando o valor presente de uma série de fluxos de caixa futuros descontados por uma taxa específica. Quando o VPL é positivo, o projeto agrega valor e teoricamente deve ser aceito; quando negativo, o projeto destrói valor e deveria ser rejeitado.

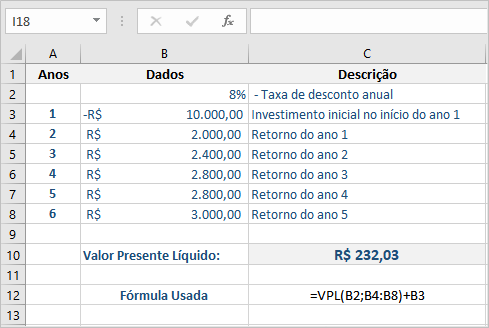
O VPL responde à pergunta fundamental de qualquer decisão de investimento: "Esse projeto vale mais do que custa?" Ao trazer todos os fluxos de caixa futuros para valor presente usando uma taxa de desconto apropriada (geralmente o custo de capital da empresa), você pode comparar objetivamente diferentes oportunidades de investimento e priorizar aquelas que geram maior retorno econômico.

Sintaxe da função VPL:

=VPL(taxa; valor1; [valor2]; ...)

Parâmetros detalhados:

• taxa: Taxa de desconto por período (custo de capital ou taxa mínima de atratividade).
• valor1, valor2, ...: Fluxos de caixa em cada período (receitas positivas, despesas negativas).
• Importante: VPL considera que fluxos ocorrem ao final de cada período; investimento inicial deve ser adicionado separadamente.

Exemplo prático 1: Análise de viabilidade de expansão empresarial:

Projeto de abertura de nova filial:
- Investimento inicial: R$ 150.000 (agora)
- Fluxo ano 1: R$ 40.000
- Fluxo ano 2: R$ 55.000
- Fluxo ano 3: R$ 70.000
- Fluxo ano 4: R$ 80.000
- Fluxo ano 5: R$ 90.000
- Taxa de desconto: 12% ao ano

Fórmula:
=-150000 + VPL(12%; 40000; 55000; 70000; 80000; 90000)

Resultado: R$ 90.542,78

Interpretação: VPL positivo de R$ 90.542,78 indica que o projeto adiciona esse valor ao patrimônio da empresa, portanto deve ser aceito.

Exemplo prático 2: Comparação entre três projetos de investimento:

Projeto	Invest. Inicial	Ano 1	Ano 2	Ano 3	Ano 4	VPL (10%)	Decisão
A	-R$ 100.000	R$ 40.000	R$ 45.000	R$ 50.000	R$ 30.000	R$ 27.658	Aceitar
B	-R$ 80.000	R$ 30.000	R$ 35.000	R$ 40.000	R$ 25.000	R$ 18.492	Aceitar
C	-R$ 120.000	R$ 35.000	R$ 40.000	R$ 40.000	R$ 35.000	-R$ 6.247	Rejeitar

Fórmula Projeto A:
=-100000 + VPL(10%; 40000; 45000; 50000; 30000)

Ranking: A > B > C (Projeto A oferece maior criação de valor)

Exemplo prático 3: Análise de substituição de equipamento:

Decisão: Trocar máquina antiga por nova?

Cenário 1 - Manter equipamento atual:
- Custo manutenção ano 1: R$ 15.000
- Custo manutenção ano 2: R$ 18.000
- Custo manutenção ano 3: R$ 22.000
VPL(8%; -15000; -18000; -22000) = -R$ 48.314

Cenário 2 - Comprar equipamento novo:
- Investimento: R$ 60.000
- Economia ano 1: R$ 25.000
- Economia ano 2: R$ 28.000
- Economia ano 3: R$ 30.000
-60000 + VPL(8%; 25000; 28000; 30000) = R$ 10.828

Conclusão: Trocar equipamento gera VPL positivo de R$ 10.828 (decisão favorável)

Tabela de sensibilidade do VPL a diferentes taxas:

Taxa de Desconto	VPL Projeto	Interpretação
8% ao ano	R$ 125.438	Altamente viável
10% ao ano	R$ 90.543	Viável
12% ao ano	R$ 60.287	Moderadamente viável
15% ao ano	R$ 18.092	Fracamente viável
18% ao ano	-R$ 15.723	Inviável

Critérios de decisão com VPL:

• VPL > 0: Projeto adiciona valor, deve ser aceito.
• VPL = 0: Projeto não agrega nem destrói valor, análise qualitativa define.
• VPL < 0: Projeto destrói valor, deve ser rejeitado.
• Comparação: Entre múltiplos projetos mutuamente exclusivos, escolha o de maior VPL positivo.

Limitações e cuidados com VPL:

• Definição da taxa: Taxa de desconto incorreta invalida toda análise; use WACC ou TMA apropriada.
• Fluxos realistas: Projeções otimistas ou pessimistas distorcem resultados drasticamente.
• Investimento inicial: Lembre-se de somar separadamente investimento inicial com sinal negativo.
• Periodicidade: Mantenha consistência entre taxa e períodos dos fluxos (ambos anuais ou mensais).

9. Função TIR: Como Calcular Taxa Interna de Retorno de Projetos

A função TIR (Taxa Interna de Retorno) calcula a taxa de desconto que faz o VPL de um projeto ser exatamente zero, representando o retorno percentual anualizado que o investimento proporcionará. A TIR é amplamente utilizada porque expressa a rentabilidade de um projeto em formato percentual facilmente comparável com outras oportunidades de investimento no mercado.

A lógica da TIR é: se a taxa calculada for superior ao custo de capital da empresa ou à taxa mínima de atratividade estabelecida, o projeto é viável e deve ser aceito. Trata-se de uma métrica intuitiva que responde "quanto esse projeto rende?" em linguagem universal de percentual de retorno, facilitando comunicação com stakeholders que podem não ter formação financeira avançada.

Sintaxe da função TIR:

=TIR(valores; [estimativa])

Argumentos explicados:

• valores: Intervalo ou matriz com série de fluxos de caixa, incluindo investimento inicial negativo.
• estimativa: [Opcional] Taxa inicial estimada para cálculo iterativo (padrão 10%).

Exemplo prático 1: TIR de investimento em startup:

Fluxo de caixa do projeto:
Ano 0 (inicial): -R$ 200.000
Ano 1: R$ 30.000
Ano 2: R$ 60.000
Ano 3: R$ 90.000
Ano 4: R$ 120.000
Ano 5: R$ 150.000

Dados em células A1:A6

Fórmula:
=TIR(A1:A6)

Resultado: 26,89% ao ano

Análise: Se o custo de capital é 15% ao ano, projeto é viável pois TIR (26,89%) supera taxa mínima exigida.

Exemplo prático 2: Comparação de três oportunidades de investimento:

Oportunidade	Invest. Inicial	Fluxos Anuais (4 anos)	TIR	Custo Capital	Decisão
Franquia A	-R$ 150.000	R$ 50k, 60k, 70k, 80k	23,7%	18%	Aceitar
E-commerce B	-R$ 100.000	R$ 35k, 40k, 45k, 50k	21,4%	18%	Aceitar
Loja Física C	-R$ 200.000	R$ 55k, 60k, 65k, 70k	14,2%	18%	Rejeitar

Ranking por TIR: Franquia A (23,7%) > E-commerce B (21,4%) > Loja C (14,2%)

Exemplo prático 3: TIR de investimento imobiliário para locação:

Análise de compra de imóvel para alugar:

Fluxo de caixa (valores em R$):
Ano 0: -450.000 (compra + reforma)
Ano 1 a 10: +36.000/ano (aluguel líquido)
Ano 10: +500.000 (venda do imóvel)

Planilha:
A1: -450000
A2:A11: 36000
A12: 536000 (aluguel + venda)

Fórmula:
=TIR(A1:A12)

Resultado: 9,87% ao ano

Interpretação: Rentabilidade de 9,87% ao ano pode ser comparada com outras aplicações imobiliárias ou financeiras.

Regra de decisão com TIR:

Se TIR > Taxa Mínima de Atratividade → ACEITAR projeto
Se TIR < Taxa Mínima de Atratividade → REJEITAR projeto
Se TIR = Taxa Mínima de Atratividade → INDIFERENTE (análise qualitativa)

TIR versus VPL - Quando podem divergir:

Situação	VPL	TIR	Critério Correto
Projetos independentes	Ambos positivos	Ambos acima TMA	Concordam - aceitar ambos
Projetos mutuamente exclusivos	A > B	B > A	Usar VPL (mais confiável)
Fluxos não convencionais	Único resultado	Múltiplas TIRs	Usar VPL sempre
Escalas diferentes	Considera magnitude	Apenas percentual	VPL melhor para tamanhos diferentes

Limitações importantes da TIR:

• Múltiplas TIRs: Projetos com múltiplas mudanças de sinal nos fluxos podem ter mais de uma TIR válida.
• TIR inexistente: Alguns padrões de fluxo não geram TIR calculável (erro #NÚM!).
• Pressuposto de reinvestimento: TIR assume que fluxos intermediários são reinvestidos à própria TIR (nem sempre realista).
• Comparação de escalas: TIR não considera tamanho do projeto, pode favorecer projetos pequenos com alta taxa.

Quando usar TIR e quando usar VPL:

• Preferir TIR: Comunicação com não-especialistas, análise individual de viabilidade, benchmarking com mercado.
• Preferir VPL: Escolha entre projetos mutuamente exclusivos, projetos de escalas muito diferentes, fluxos complexos.
• Usar ambos: Análise completa deve incluir VPL E TIR para visão mais robusta da viabilidade.

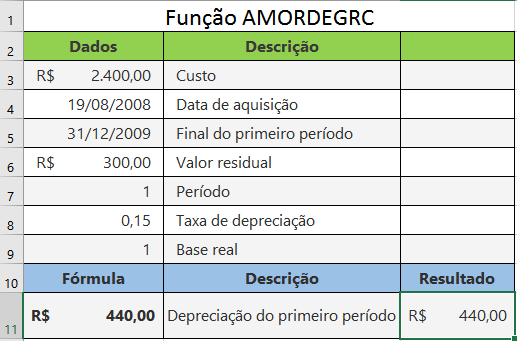
10. Funções de Depreciação: BD, BDD e SLN Para Ativos

As funções de depreciação do Excel calculam a perda de valor de ativos ao longo de sua vida útil, essenciais para contabilidade, planejamento tributário e análise financeira de investimentos em bens duráveis. O Excel oferece diferentes métodos de depreciação que atendem normas contábeis brasileiras e internacionais, permitindo escolher o mais adequado para cada situação específica.

A depreciação representa o desgaste, deterioração ou obsolescência de bens tangíveis utilizados na operação empresarial. Calcular corretamente a depreciação é fundamental para determinar o valor contábil real dos ativos, calcular custos operacionais precisos e apurar o lucro tributável de acordo com legislação fiscal vigente no Brasil.

Função SLN - Depreciação Linear (Mais Comum):

=SLN(custo; residual; vida_útil)

Parâmetros:

• custo: Valor inicial de aquisição do ativo.
• residual: Valor estimado ao final da vida útil (valor de revenda).
• vida_útil: Número de períodos durante os quais o ativo será depreciado.

Exemplo prático com SLN:

Compra de veículo comercial:
- Custo de aquisição: R$ 80.000
- Valor residual após 5 anos: R$ 20.000
- Vida útil: 5 anos

Fórmula:
=SLN(80000; 20000; 5)

Resultado: R$ 12.000 por ano

Depreciação mensal: R$ 12.000 / 12 = R$ 1.000

Tabela de depreciação linear:

Ano	Valor Inicial	Depreciação Anual	Depreciação Acumulada	Valor Contábil
1	R$ 80.000	R$ 12.000	R$ 12.000	R$ 68.000
2	R$ 68.000	R$ 12.000	R$ 24.000	R$ 56.000
3	R$ 56.000	R$ 12.000	R$ 36.000	R$ 44.000
4	R$ 44.000	R$ 12.000	R$ 48.000	R$ 32.000
5	R$ 32.000	R$ 12.000	R$ 60.000	R$ 20.000

Função BD - Depreciação com Saldo Decrescente:

=BD(custo; residual; vida_útil; período; [mês])

Parâmetros adicionais:

• período: Ano específico para o qual calcular a depreciação.
• mês: [Opcional] Número de meses no primeiro ano (padrão 12).

Exemplo com BD:

Equipamento industrial:
- Custo: R$ 150.000
- Residual: R$ 30.000
- Vida útil: 8 anos
- Método: Saldo decrescente

Depreciação ano 1:
=BD(150000; 30000; 8; 1)
Resultado: R$ 31.689,35

Depreciação ano 2:
=BD(150000; 30000; 8; 2)
Resultado: R$ 24.962,54

Comparação entre métodos de depreciação:

Método	Característica	Quando Usar
SLN (Linear)	Valor constante todos anos	Ativos com desgaste uniforme
BD (Saldo Decrescente)	Maior no início, menor no fim	Equipamentos tecnológicos
BDD (Duplo Decrescente)	Acelerada nos primeiros anos	Veículos e máquinas

Função BDD - Depreciação Dupla Decrescente:

=BDD(custo; residual; vida_útil; período; [fator])

Exemplo com BDD:

Computadores e servidores:
- Custo total: R$ 200.000
- Residual: R$ 20.000
- Vida útil: 5 anos

Ano 1: =BDD(200000; 20000; 5; 1) = R$ 80.000
Ano 2: =BDD(200000; 20000; 5; 2) = R$ 48.000
Ano 3: =BDD(200000; 20000; 5; 3) = R$ 28.800
Ano 4: =BDD(200000; 20000; 5; 4) = R$ 17.280
Ano 5: =BDD(200000; 20000; 5; 5) = R$ 5.920

Taxas anuais de depreciação segundo Receita Federal (referência):

Tipo de Ativo	Taxa Anual	Vida Útil
Edifícios	4%	25 anos
Móveis e utensílios	10%	10 anos
Máquinas e equipamentos	10%	10 anos
Veículos	20%	5 anos
Computadores	20%	5 anos
Ferramentas	15%	6,67 anos

Aplicações práticas da depreciação:

• Balanço patrimonial: Determinar valor contábil correto dos ativos imobilizados.
• Demonstrativo de resultados: Calcular despesa de depreciação que reduz lucro tributável.
• Planejamento tributário: Escolher método de depreciação que otimize carga fiscal legalmente.
• Análise de substituição: Decidir momento ideal para trocar equipamentos baseado em valor residual.

Como Usar Funções Financeiras Para Análise de Rentabilidade

A combinação estratégica de múltiplas funções financeiras do Excel permite criar análises sofisticadas de rentabilidade que orientam decisões de investimento com base em dados concretos e cenários realistas. Integrar VP, VF, VPL, TIR e outras funções em modelos financeiros completos transforma o Excel em poderosa ferramenta de inteligência empresarial.

Modelo completo de análise de investimento:

Análise de abertura de nova unidade de negócio:

PREMISSAS:
- Investimento inicial: R$ 300.000
- Receita mensal estimada: R$ 80.000
- Custos operacionais mensais: R$ 55.000
- Margem mensal: R$ 25.000
- Prazo de análise: 5 anos (60 meses)
- Taxa de desconto: 1% ao mês (12,68% ao ano)

FÓRMULAS:

1. Fluxo de caixa mensal livre:
Receitas - Custos = R$ 25.000/mês

2. VPL do projeto:
=-300000 + VPL(1%; arrastar 60 células com 25000)
Resultado: R$ 848.372,45

3. TIR mensal:
=TIR(investimento inicial + 60 fluxos mensais)
Resultado: 7,45% ao mês

4. TIR anual equivalente:
=(1+7,45%)^12-1 = 142,1% ao ano

5. Payback (recuperação do investimento):
=NPER(1%; -25000; 300000; 0)
Resultado: 14,3 meses

6. Valor futuro acumulado após 5 anos:
=VF(1%; 60; -25000; -300000)
Resultado: R$ 2.381.475,38

Análise de sensibilidade em diferentes cenários:

Cenário	Margem Mensal	VPL	TIR Anual	Payback	Decisão
Pessimista	R$ 18.000	R$ 311.748	98,3%	19,2 meses	Aceitar com ressalvas
Realista	R$ 25.000	R$ 848.372	142,1%	14,3 meses	Aceitar fortemente
Otimista	R$ 32.000	R$ 1.384.997	185,7%	11,1 meses	Aceitar com alta prioridade

Dashboard financeiro integrado:

INDICADORES DE VIABILIDADE:

Critério 1 - VPL:
Status: POSITIVO (R$ 848.372,45)
Conclusão: Projeto adiciona valor significativo

Critério 2 - TIR:
Status: 142,1% > 20% (TMA)
Conclusão: Retorno supera custo de capital

Critério 3 - Payback:
Status: 14,3 meses < 24 meses (limite)
Conclusão: Recuperação rápida do investimento

Critério 4 - Índice de Lucratividade:
IL = (VPL + Investimento) / Investimento
IL = (848.372 + 300.000) / 300.000 = 3,83
Conclusão: Cada R$ 1 investido gera R$ 3,83

RECOMENDAÇÃO FINAL: APROVADO

Análise de break-even (ponto de equilíbrio):

Determinar margem mensal mínima para VPL = 0:

Usar Atingir Meta:
- Célula objetivo: VPL
- Valor desejado: 0
- Célula variável: Margem mensal

Resultado: R$ 6.892/mês

Interpretação: Projeto começa a destruir valor se margem cair abaixo de R$ 6.892 mensais

Comparação de múltiplos projetos concorrentes:

Projeto	Invest.	VPL	TIR	Payback	IL	Ranking
Expansão Norte	R$ 300k	R$ 848k	142%	14,3m	3,83	1º
Loja Shopping	R$ 450k	R$ 672k	98%	22,1m	2,49	3º
E-commerce	R$ 180k	R$ 534k	165%	9,8m	3,97	2º
Franquia Sul	R$ 250k	R$ 412k	115%	16,4m	2,65	4º

Decisão: Expandir Norte (melhor VPL absoluto) e E-commerce (melhor TIR e IL com menor investimento).

Fórmulas auxiliares para análise completa:

ROI (Retorno sobre Investimento):
=((VF - Investimento) / Investimento) * 100

Margem de Segurança:
=(Receita Esperada - Break-even) / Receita Esperada

Razão Benefício/Custo:
=SOMA(Fluxos Positivos VP) / SOMA(Fluxos Negativos VP)

Conclusão

As funções financeiras do Excel são ferramentas indispensáveis para qualquer profissional que lida com análise de investimentos, planejamento financeiro ou gestão empresarial. Dominar essas funcionalidades transforma completamente sua capacidade de avaliar oportunidades, comparar alternativas e tomar decisões fundamentadas em dados precisos e cálculos matemáticos sólidos que eliminam suposições e achismos prejudiciais.

Ao longo deste guia completo, você aprendeu não apenas a sintaxe técnica de cada função, mas principalmente como aplicá-las em situações reais do cotidiano profissional. Desde cálculos básicos de parcelas de financiamento até análises sofisticadas de viabilidade econômica com VPL e TIR, essas ferramentas elevam significativamente o nível das suas entregas e demonstram competência técnica que diferencia profissionais no mercado competitivo atual.

A prática constante com exemplos diversos consolidará seu conhecimento e desenvolverá a intuição necessária para escolher rapidamente qual função usar em cada situação específica. Crie suas próprias planilhas de simulação, experimente diferentes cenários e construa modelos financeiros personalizados que atendam às necessidades particulares do seu negócio ou área de atuação para maximizar resultados financeiros sustentáveis.

Perguntas Frequentes

1. Qual a diferença entre VP e VPL no Excel e quando usar cada função?

A função VP calcula o valor presente de pagamentos periódicos regulares com ou sem valor futuro final, sendo ideal para analisar financiamentos e investimentos com fluxos constantes. Já VPL calcula valor presente líquido de fluxos irregulares variáveis ao longo do tempo, melhor para avaliar projetos com receitas e despesas diferentes em cada período.

2. Como calcular a prestação de um financiamento incluindo seguro e outras tarifas?

Use a função PGTO normalmente, mas some todas as tarifas mensais fixas ao resultado final. Para tarifas únicas iniciais, subtraia-as do valor financiado antes de calcular. Exemplo: se financia R$ 100.000 com tarifa de R$ 2.000, calcule PGTO usando R$ 98.000 como valor presente para obter prestação real considerando todos custos.

3. Por que minha função TIR retorna erro #NÚM! no Excel?

O erro ocorre quando o Excel não consegue convergir para uma solução após 20 iterações, geralmente devido a fluxos de caixa com múltiplas mudanças de sinal ou padrões incomuns. Tente fornecer estimativa inicial diferente no segundo parâmetro da função (por exemplo, 5% ou 20%) ou verifique se há erros nos valores do fluxo de caixa.

4. Como transformar taxa de juros mensal em anual e vice-versa no Excel?

Para converter mensal em anual use a fórmula: =(1+taxa_mensal)^12-1. Para converter anual em mensal: =(1+taxa_anual)^(1/12)-1. Por exemplo, 1% ao mês equivale a =(1+1%)^12-1 = 12,68% ao ano. Nunca multiplique ou divida diretamente, pois juros compostos requerem exponenciação matemática correta.

5. Posso usar funções financeiras para calcular investimentos com aportes irregulares?

Sim, use a função XVPL para fluxos com datas específicas irregulares, ou organize fluxos mensais colocando zero nos meses sem aporte. Para TIR com datas específicas, utilize XTIR. Essas funções aceitam dois intervalos: um com valores e outro com datas correspondentes, calculando corretamente mesmo quando períodos não são uniformes.